NUMBER TOLERANCE And Its Role IN THE GEOMETRY OF FORM
NUMBER TOLERANCE And Its Role IN THE GEOMETRY OF FORM

Builders learn quickly that measurement, though essential to their craft, nonetheless can never be exact. No matter how much care is taken, (in practice) it is impossible to cut anything precisely, or perfectly, in half. No tool can ever be devised that would enable us to cut one thing into two pieces such that each halves’ measurement could accurately be described by the same number. For if measurement could be precise to enough decimal points, sooner or later a discrepancy in size would be detected.
For framing a quality house in wood this may require all of the pieces to be within 1/16 of an inch (of designed measurement) for the resulting building to come out straight and smooth. For a cylinder to operate properly in an internal combustion engine the pieces must conform to within 1/10,000 of an inch. More sophisticated devices require even greater precision; yet, none expect nor require exactitude.
In Geometry, with its inherent system of formal relationships, tolerance plays an essential role. For example, a 1.0 volume-unit in the form of a sphere has a radius described by the number:
0.6203505…
And a 1.0 surface-unit in the form of a tetrahedron has its height described by the number:
0.6204031
These certainly are different numbers, but their difference is very slight. Their congruence extends through the first four number places (0.6203505…/0.6204031 = 0.99991…) which means these numbers are the same quantity until after the fourth decimal place. Thus the Unit, in its form as a spherical volume; and the Unit, in its form as a tetrahedron’s surface are (within a certain tolerance) commensurate forms.

As illustrated here, these two easily modeled three dimensional forms are exquisitely related within the bounds of the same focal plateau. Expressed graphically, this concept might resemble the convergence of the two lines below.

Thus the idea of a focal point draws an analogy with this idea of number congruence, or near congruence. If nature in some manner is using the Unit-volume sphere, and the Unit-surface tetrahedron as available building materials for cosmic constructions, the (near) congruence of these two measures could be artfully employed within the bounds of their parallel tolerance.
Another good example illustrating these built-in commensurate bounds of geometry can be seen by way of a further introduction to what I have come to call the “Transitional-tetrahedron” (a.k.a., “Transit-tet”, or “T-tet” for convenience). This form arises under the following conditions.
Imagine 1.0 surface-unit in the form of a sphere. If two of these identical surface units combine their volumes into one spherical unit, then excess surface area needs to be ejected. This excess surface area is modeled by the surface area of a regular tetrahedron. . . i.e., the “Transitional-tetrahedron. Its volume is:
0.01370203224…
Now if instead, one of those same spheres divides its 1.0 surface-unit into the surfaces of two new spherical units, then excess volume must be ejected in the transformation. This excess volume quantity is packaged in the form of two identical “Transitional-tetrahedrons”. The volume of this form of the Transit-tetrahedron is:
0.0137706087…
So beginning with the same 1.0 surface-unit in the form of a sphere, we see two completely opposite transformations use the same geometric form to account for the resulting surface and volume inequalities which arise as a result of geometry’s “packaging economies”.
The cross-section of the 1.0 surface-unit sphere is a circle. The largest equilateral triangle that fits perfectly within this circle’s circumference is the face of a regular tetrahedron. This tetrahedron is the ideal form of the Transitional-tetrahedron. Its volume is:
0.0137467754…
There is one other Transitional-tetrahedron that has appeared with great significance in The Geometry of Form. This arises with the transformation of a seven point system into an eight point system (i.e., the Decahedron, modeling Unity’s system of seven points of potential, transforms into the actualized eight points of the Star-tetrahedron). Much more will be said about these characters and their transformations throughout this text, but for purposes here it is sufficient to know that the difference in volume between these two systems is:
0.0137500069…
and modeled in the form of a regular tetrahedron it becomes another form of the “T-tet”.
Clearly, these four tetrahedrons are the same tetrahedron within the bounds of the ten-thousandths number place. This boundary might be termed “the commensurate bounds of The Geometry of Form”. This is to say that geometry itself is imperfect when scrutinized beyond its built-in commensurate limits. But within the bounds of this focal point, this tolerance, the forms of geometry are commensurate.
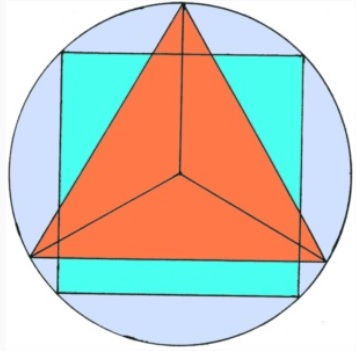
The drawing above provides us with further insights into the workings of number congruence within the idealized system of geometric forms. The circle represents the cross-section of the spherical 1.0 surface-unit. Its radius measure is 0.2820947… The equilateral triangle within the circle appears to be tangent to the circle’s circumference when in fact the lineal measure from the triangle’s center to its respective corners is 0.2817994… This particular triangle represents one of the four faces of the Transit-tetrahedron which perfectly models the excess surface ejected when two of the 1.0 surface-unit spheres fuse their volumes into one single sphere.
There is no disputing that this particular tetrahedron is intimately related to this specific sphere since its very existence was born from the need to balance the surface differential arising from fusing two of these spherical volumes. But even without this knowledge, from the seemingly obvious congruence alone, one could deduce that the two forms were related. Not until the drawing is enlarged sufficiently in scale could we determine visually their miniscule difference. And this difference would grow more and more apparent as the scale is increased relative to us, the observers.
The square in the drawing is another example of this tolerance built into the structuring of geometry. It represents one face of 1.0 surface-unit (this time) in the form of a cube. Like the tetrahedron’s face, this cube’s face also appears to be congruent with the circle’s circumference. Both of these form’s apparent visual congruence, and the fact that they are both scaled to the same 1.0 surface-unit, would lead one to conclude that these idealized forms of geometry are united within one system of quanta-sization. But again, it is only when the specific measurements are scrutinized beyond the designed tolerance do we see that the cube’s face radial length of 0.2886751… is slightly greater than the sphere’s radius. This difference is practically indiscernible on the scale of this drawing.
In this next drawing these forms have been rendered three-dimensionally. The figure on the left shows the 1.0 surface-unit cube and the sphere intermeshed. The cube fits nicely with the sphere, with its edge mid-points appearing to just touch the sphere. The figure on the right shows the cube delineated by its diagonal planes, this time sitting atop the cross-section of the 1.0 surface-unit sphere. The tetrahedron set on the sphere’s cross-section and intermeshed with the planes of the cube is the ideal form of the Transitional-tetrahedron. It appears to just touch the upper face of the cube. In fact, the cube’s height measures 0.4082482… while the height of the tetrahedron is 0.3989422… (which is also the radius of a 2.0 surface-unit sphere; meaning that this tetrahedron fits perfectly within a hemisphere equal to 1.0 surface-unit).
Now when I make the statement that geometry itself is imperfect, what I mean by that is this: If geometry was perfect we would expect that the transitional-tetrahedron (0.0137706087…) accounting for the volume discrepancy when dividing the surface of the 1.0 surface-unit sphere to be the same transitional-tetrahedron (0.01370203224…) that accounts for the surface discrepancy when fusing two such volumes. They certainly are not the same. Yet within a certain tolerance defining the commensurate bounds of The Geometry of Form, they are the same. Again, the same logic applies to the previous modeling of the 1.0 surface-unit cube and sphere. If geometry was perfect we would expect the sphere’s radius (0.2820947…) to be described by precisely the same number as half the cube’s face diagonal (0.2817994…); and the T-tet’s height (0.3989422…) to be the same as the height of the cube. They are not. But within the focal point inherent to this system of geometric forms, they can be regarded as the same.
Now out of this chaos of apparent non-commensuration there is an underlying order to the variance among the forms. We find that the cube and sphere vary from their implied ideals:
(0.28209…/0.28867… = 0.97720…)
in the same proportion as that found between the height of the tetrahedron and cube:
(0.39894…/0.40824… = 0.97720…)
Moreover, this same ratio (0.97720…) describes the difference in volume between the aforementioned, Transitional-tetrahedron generating, Decahedron/Star-tetrahedron transformation. This number sequence, divided in half (0.97720…/2 = 0.4886…) results in the edge length of the ideal Transitional-Tetrahedron.
There are many other examples which appear in other contexts throughout the Geometry of Form which show in every instance this focal plateau. It is as if the system were inherently imperfect if scrutinized too closely, yet completely commensurate within the focal range.
~Paul Kasprzycki
Order Paul’s Book’s Here
